lunes, 26 de noviembre de 2018
domingo, 25 de noviembre de 2018
Hiperbola
2) ECUACIÓN DE LA HIPERBOLA:
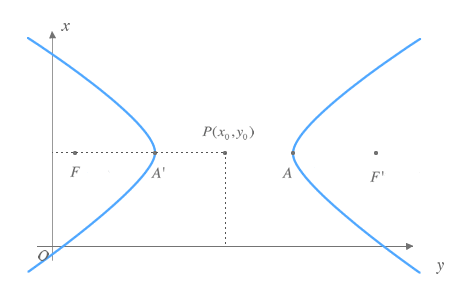
Hipérbola de eje focal horizontal centrada en un punto P(x0,y0) cualquiera:
La ecuación de una hipérbola eje focal horizontal viene dada por:
Hipérbola de eje focal vertical centrada en un punto P(x0,y0) cualquiera:
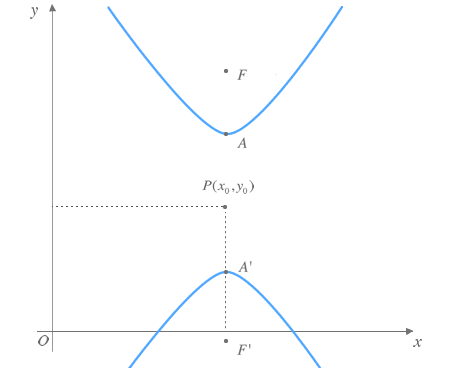
La ecuación de una hipébola de eje focal vertical viene dada por:
Hiperbole
1) DEFINICIÓN DE HIPERBOLA: Una hiperbola se define como el lugar geométrico de los puntos del plano en el que la diferencia de distancias a dos puntos fijos denominados focos, F y F', es siempre constante.
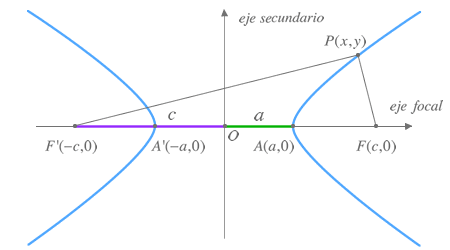

Elementos de la hipérbola:
- Focos (F y F'). Puntos fijos en los que la diferencia de distancia entre ellos y cualquier punto de la hipérbola es siempre la misma.
- Eje focal, principal o real. Recta que pasa por los focos.
- Eje secundario o imaginario. Mediatriz del segmento que une los dos focos.
- Centro (O). Punto de intersección de los ejes focal y secundario.
- Semidistancia focal (c). La mitad de la distancia entre los dos focos F y F'. Su valor es c.
- Distancia focal (2c). Distancia del segmento que une los dos focos F y F'. Su longitud es 2c.
- Los vértices (A y A'). Puntos de la hipérbola que cortan al eje focal.
- Semieje real (a). Segmento que va desde el origen O hasta cuaqluiera de los vertices A o A'. Su longitud es a.
- Semieje imaginario (b).
b=c2−a2−−−−−−√
Ejercicios sobre la Parábola
1) Determina las ecuaciones de las parábolas que tienen:
a) De directriz x = -3, de foco (3, 0).





a) De directriz x = -3, de foco (3, 0).

p= d(F.r)=6
y²= 12x
b)De directriz y = 4, de vértice (0, 0).

p/2= 4
x²= -16y
2)Hallar la ecuación de la parábola de eje vertical y que pasa por los puntos: A(6, 1), B(-2, 3), C(16, 6).
y= ax² + bx+ c



Créditos: https://www.vitutor.com/geo/coni/iActividades.html?fbclid=IwAR1GoK8XJwVvvFXQCPlWMHeKixoT4-HGBJmjQvXxNShDtu1FhZNPnuOohH8
sábado, 24 de noviembre de 2018
Parábola 3
1) La ecuación de la parábola con vértice en el origen y eje focal sobre el eje X
que abre hacia la derecha es:

2) La ecuación de la parábola con vértice en el origen y eje focal sobre el eje X
que abre hacia la izquierda es:

3) La ecuación de la parábola con vértice en el origen y eje focal sobre el eje Y
que abre hacia abajo es:

4) La ecuación de la parábola con vértice en el origen y eje focal sobre el eje Y
que abre hacia arriba es:

Parábola 2
Desarrollamos la ecuación canónica:
x 2 – 2hx + h 2 = 4py – 4pk
x 2 – 2hx + h 2 – 4py + 4pk = 0
Multiplicando la ecuación por un coeficiente “A” con la intención de generalizar, y considerando A ≠ 0 , tendremos:
Ax 2 – 2Ahx + Ah 2 – 4Apy + 4Apk = 0
Reordenando:
Ax 2 – 4Apy – 2Ahx – Ah 2 + 4Apk = 0
Ax 2 – 4Apy – 2Ahx + A(h 2 + 4pk) = 0
Haciendo que los coeficientes de las variables sean:
– 4Ap = B
– 2Ah = C
A(h 2 + 4pk) = D
Ahora reemplazando tendremos lo siguiente:
Ax 2 + Bx + Cy + D = 0
Para una parábola de orientación vertical, la ecuación en su forma general será:
Ay 2 + Bx + Cy + D = 0
Parábola
a) Definición de parábola: Una parábola queda definida por el conjunto de los puntos del plano que equidistan de una recta fija y un punto fijo:
d(P,D)=d(P,F)
b) Elementos de la parábola:
*Foco: Es el punto fijo F.
*Directriz: Es la recta fija D.
*Parámetro: Es la distancia entre el foco y la directriz de la parábola, se le denomina P.
*Eje: Es la recta perpendicular a la directriz y que pasa por el foco, es el eje de simetría de la parábola.
*Vértice: Es el punto medio entre el foco y directriz.
* Radio Vector: Es el segmento que une un punto de la parábola con el foco.
c) Obtención de la ecuación general de la parábola:
-Para obtener dicha ecuación es necesario desarrollar la forma ordinaria o canónica de la ecuación:
(x – h) 2 = 4p(y – k)
Suscribirse a:
Entradas (Atom)